 1. Rumus Jumlah dan selisih dua sudut
1. Rumus Jumlah dan selisih dua sudut
Cos α = x/r => x = r cos α
Sin α = y/r => y = r sin α
Koordinat kutub : P (r cos α , r sin α)
(cos β , sin β )
= (cos α , sin α )
= (cos β - cos α)2 + (sin β - sin α)2
= (cos2 β - 2 cos α cos β + cos2 α) + ( sin2 β - 2 sin α sin β + sin2 α)
= 2 - 2 sin α sin β - 2 cos α cos β
3. ATURAN COSINUS
AB2 = OA2 + OB2 - 2.OA.OB cos p
= 1 + 1 - 2.1.1 cos (β - α)
2 - 2 cos (β - α) = 2 - 2 cos β cos α - 2 sin β sin α
Jadi, cos (β - α) = cos β cos α + sin β sin α
cos (α - β) = cos α cos β + sin α sin β
Rumus2 :
1. cos (A + B) = cos {A -(-B)}
= cos A cos (-B) + sin A sin (-B)
= cos A cos B + sin A . - sin B
= cos A cos B - sin A sin B
2. sin (A + B) = cos {90° - (A + B)}
= cos {(90° - A) - B}
= cos (90° - A) cos B + sin (90° - A) sin B
= sin A cos B + cos A sin B
3. sin (A - B) = sin {A +(-B)}
= sin A cos (-B) + cos A sin (-B)
= sin A sin B - cos A sin B
Contoh Soal :
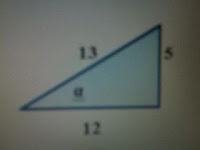
1. sin α = 5/13 dan cos β = 4/5
α tumpul dan β lancip
Tentukan nilai dari sin (α - β)!
Jawaban :
dari gambar, cos α = -12/13
sin β = 3/5
sin (α - β) = sin α cos β - cos α sin β
= 5/13 . 4/5 - (-12/13) . 3/5
= 20/65 + 36/65
= 56/65
4. RUMUS TAN (α ± β)
a. tan (α + β)
= sin (α + β) / cos (α + β)
= (sin α cos β + cos α sin β) / (cos α cos β - sin α sin β)
= {(sin α cos β) / (cos α cos β)} + {(cos α cos β) / (cos α cos β)}
{(cos α cos β) / (cos α cos β)} - {(sin α cos β) / (cos α cos β)}
= tan α + tan β
1 - tan α tan β
Jadi, tan (α + β) = tan α + tan β
1 - tan α tan β
tan (α - β) = tan α - tan β
1 + tan α tan β

Contoh Soal :
1. Jika sin A = 3/s dan cos B = 12/13
< A di kuadran II dan < B di kuadran I
Tentukan nilai dari tan (A + B)
Jawaban :

dari gambar, maka tan A = -3/5 dari gambar maka tan B = 5/12
maka, tan (A + B) = tan A + tan B
1 - tan A tan B
= -3/4 + 5/12
1 - (-3/4) . 5/12
= -4/12
21/16
= -16/63
5. Rumus Fungsi Trigonometri Sudut Rangkap
* α + β + γ = 180°
* α + β = 180° - γ
a. Sin 2A = Sin (A + A)
= Sin A cos A + Cos A Sin A
Jadi, Sin 2A = 2 Sin A Cos A
b. Cos 2A = Cos (A + A)
= Cos A cos A - Sin A Sin A
Jadi, Cos 2A = Cos2 A - Sin2 A
c. Tan 2A = Tan (A + A)
= Tan A + Tan A
1 - Tan A Tan A
Jadi, Tan 2A = 2 Tan A
1 - Tan A Tan A
1. Sin (A + B) = Sin A Cos B + Cos A Sin B
2. Sin (A - B) = Sin A Cos B - Cos A Sin B
(+) Sin (A + B) + Sin (A - B) = 2 Sin A Cos B ...(1)
(-) Sin (A + B) - Sin (A - B) = 2 Cos A Sin B ...(2)
1. Cos (A + B) = Cos A Cos B - Sin A Sin B
2. Cos (A - B) = Cos A Cos B + Sin A Sin B
(+) Cos (A + B) + Cos (A - B) = 2 Cos A Cos B ...(3)
(-) Cos (A + B) + Cos (A - B) = -2 Sin A Sin B ...(4)
Jadi, diperoleh :
1. Sin (A + B) + Sin (A - B) = 2 Sin A Cos B
2. Sin (A + B) - Sin (A - B) = 2 Cos A Sin B
3. Cos (A + B) + Cos (A - B) = 2 Cos A Cos B
4. Cos (A + B) + Cos (A - B) = -2 Sin A Sin B
Maka,
1. Sin C + Sin D = 2 Sin C + D Cos C - D
2 2
2. Sin C - Sin D = 2 Cos C + D sin C - D
2 2
3. Cos C + Cos D = 2 Cos C + D Cos C - D
2 2
4. Cos C - Cos D = -2 Sin C + D Sin C - D
2 2
* A + B = C * A + B = C
A - B = D + A - B = D -
2A = C + D 2B = C - D
A = C + D B = C - D
2 2
Maka,
1. Sin C + Sin D = 2 Sin C + D Cos C - D
2 2
2. Sin C - Sin D = 2 Cos C + D sin C - D
2 2
3. Cos C + Cos D = 2 Cos C + D Cos C - D
2 2
4. Cos C - Cos D = -2 Sin C + D Sin C - D
2 2





7 April 2016 pukul 07.25
thx utk ilmunya