* PERTIDAKSAMAAN KUADRAT *
Menentukan Himpunan Penyelesaian (HP) dari pertidaksamaan kuadrat
menggunakan langkah2 berikut :
1. Ubahlah pertidaksamaan menjadi persamaan
2. Tentukan akar2 dari persamaan kuadrat tersebut.
3. Tentukan letak akar2 persamaan kuadrat pada garis bilangan.
4. Tentukan daerah + dan daerah -
5. Tulislah HP sesuai soal yang diminta
Contoh Soal :
Tentukan HP dari pertidaksamaan berikut
Jawaban :
a. x2 – 2x - 3 = 0
a. x2 – 2x - 3 = 0
b. (x - 3) (x + 1) = 0,
maka x = 3,-1
maka x = 3,-1
c. dan d. Gambar disamping
yang diminta (≤) maka daerahnya (-)
yang diminta (≤) maka daerahnya (-)
e. HP {x│-1 ≤ x ≤ 3}

2. -2x2 – 11x - 15 < 0

2. -2x2 – 11x - 15 < 0
Jawaban :
a. -2x2 – 11x - 15 = 0
b. (2x - 5) (-x + 3) =0,
maka x = 5/2,3
c. dan d. gambar disamping
yang diminta (<) maka daerahnya (-)
yang diminta (<) maka daerahnya (-)
e. HP {x│x < 5/2 , x > 3}
Langkah Penyelesaian :
3. x2 – 4x + 4 < 0
a. x2 – 4x + 4 = 0
b. (x - 2)2 = 0
maka x = 2
misal x = 3 => (3 - 2)2 = 1 (+)
x = 1 => (1 - 2)2 = 1 (+)
c. dan d. gambar disamping
yang diminta (<) maka daerahnya (-)
yang diminta (<) maka daerahnya (-)
e. HP { } atau Himpunan Kosong
* PERTIDAKSAMAAN LINEAR *
Sifat2 :
1. a < b <=> b > a
2 < 5 <=> 5 > 2
2. a < b <=> ac < bc untuk c > 0
2 < 5 <=> 2(3) < 5(3)
3. a < b <=> ac > bc untuk c < 0
2 < 5 <=> 2(-1) > 5(-1)
4. a< b <=> a+c < b+c
2 < 5 <=> 2+5 < 5+5
2 < 5 <=> 2+(-3) < 5+(-3)
Contoh Soal :
1. x - 5 < 3x + 4
Jawaban :
x - 3x < 4 + 5
- 2x < 9
x > -9/2
Jadi, HP {x│x > -9/2}
2. -6 < 2x ≤ 10
Jawaban :
-6 < 2x dan 2x ≤ 10
2x > -6 x ≤ 5
x > -3
maka HP {x│-3 < x ≤ 5}
3. {(3x -5)/5} ≤ {(2 + 3x)/4}
Jawaban :
masing2 ruas (x20)
4(3x - 5) ≤ 5(2 + 3x)
12x - 20 ≤ 10 + 15x
12x - 15x ≤ 10 + 20
-3x ≤ 30
x ≥ -10
maka, HP {x│x ≥ -10}4. {(7x - 5)/-5} ≥ {(3x - 3)/2}
Jawaban :
masing2 ruas (x10)
-2(7x - 5) ≥ 5(3x - 3)
-14x + 10 ≥ 15x - 15
-14x - 15x ≥ -15 - 10
-29x ≥ -25
x ≤ 25/29
Maka, HP {x│x ≤ 25/29}
5. (x/3) - 2 ≥ 1
Jawaban :
masing2 ruas (x3)
3(x/3) - 2(3) ≥ 1(3)
x - 6 ≥ 3
x ≥ 3 + 6
x ≥ 9
Maka, HP {x│x ≥ 9}
6. {(-2x - 5)/-3} ≥ -4
Jawaban :
masing2 ruas (x-3)
(-2x - 5) ≥ -4(-3)
-2x - 5 ≥ 12
-2x ≥ 12 + 5
-2x ≥ 17
x ≤ -17/2
Maka, HP {x│x ≤ -17/2}
7. 2 - x ≤ {(3x - 3)/4} ≤ (2x + 3)
Jawaban :
{(3x - 3)/4} ≥ 2 - x dan {(3x - 3)/4} ≤ 2x + 3
masing2 ruas (x4) masing2 ruas (x4)
3x - 3 ≥ 4(2 - x) 3x - 3 ≤ 4(2x + 3)
3x - 3 ≥ 8 - 4x 3x - 3 ≤ 8x + 12
3x + 4x ≥ 8 + 3 3x - 8x ≤ 12 + 3
7x ≥ 11 -5x ≤ 15
x ≥ 11/7 x ≥ -3
maka, HP {x│x ≥ 11/7}
Menyelesaikan Pertidaksamaan Pecahan Bentuk Linear
Contoh : {(ax + b)/(cx + d)} < 0
Langkah Penyelesaian :
1. Tentukan pembuat nol (0) pembilang
2. Tentukan pemuat nol (0) penyebut, cx + d ≠ 0
3. Tentukan pembuat nol pembilang dan penyebut pada garis bilangan
4. Tentukan daerah (+) dan (-)
5. Tentukan HP
Contoh Soal :
Jawaban :
a. 2x + 3 = 0 dan b. x - 4 = 0
2x = -3 x = 4
x = -3/2
c. dan d. pada gambar di samping
yang diminta (≥) maka daerahnya (+)
yang diminta (≥) maka daerahnya (+)
e. HP {x│x ≤ -3/2 atau x > 4}
2. {(2x - 5)/(x - 3)} ≤ 1
Jawaban :
{(2x - 5)/(x - 3)} - {(x - 3)/(x - 3)} ≤ 0
{(2x - 5 - x + 3)/(x - 3) ≤ 0
{(x - 2)/(x - 3)} ≤ 0
a. x - 2 = 0 dan b. x - 3 = 0
x = 2 x = 3
c. dan d. pada gambar di samping
yang diminta (≤) maka daerahnya (-)
yang diminta (≤) maka daerahnya (-)
e. HP {x│2 ≤ x < 3}
3. {(2x + 5)/(1 - x)} > 1
Jawaban :
{(2x + 5)/(1 - x)} - {(1 - x)/(1 - x)} > 0
{(2x + 5 - 1 + x)/(1 - x)} > 0
{(3x + 4)/(1 - x)} > 0
a. 3x + 4 = 0 dan b. 1 - x = 0
3x = -4 -x = -1
x = -4/3 x = 1
c. dan d. pada gambar di samping
yang diminta (>) maka daerahnya (+)
yang diminta (>) maka daerahnya (+)
e. HP {x│-4/3 ≤ x < 1}
Menyelesaikan Pertidaksamaan Bentuk Kuadrat
a. 4x - 2 = 0 dan b. (x - 2)(x - 4) = 0
Contoh : {(ax2 + bx +c)/(px2 + qx + r)} ≤ 0
Keterangan : Untuk langkah2 penyelesaian bisa melihat langkah2
penyelesaian pada persamaan bentuk linear.
Contoh Soal :
1. {(x - 1) /(x - 2)} ≤ {(x + 1)/(x + 4)}
Jawaban:
[{(x - 1)(x + 4)-(x + 1)(x - 2)}/(x - 2)(x - 4)]≤ 0
[{(x2+3x-4)-(x2-x-2)}/(x-2)(x-4)]≤ 0
{(4x - 2)/(x - 2)(x - 4)}≤ 0
a. 4x - 2 = 0 dan b. (x - 2)(x - 4) = 0
4x = 2 x = 2 , x = 4
x = 1/2
c. dan d. pada gambar di samping
c. dan d. pada gambar di samping
yang diminta (≤) maka daerahnya (-)
e. HP {x│x < -1/4 atau 1/2 ≤ x < 2, x € R}
Jawaban :
a. x - 3 = 0 atau x + 2 = 0
x = 3 x = -2
b. 2x - 1 = 0 atau 4 - x = 0
x = 1/2 x = 4
c. dan d. pada gambar di samping
yang diminta (≥) maka daerahnya (+)
e. HP {x│-2 ≤ x < 1/2 atau 3 ≤ x < 4}
3. {(x2 + x - 6)/(-x2 + 5x - 4)} < 0
{(x + 3)(x - 2)/(-x + 1)(x - 4)} < 0
a. x + 3 = 0 atau x - 2 = 0
x = -3 x = 2
b. -x + 1 = 0 atau x - 4 = 0
x = 1 x = 4
c. dan d. pada gambar di samping
yang diminta (<) maka daerahnya (-)
e. HP {x│x ≤ -3 , 1 < x ≤ 2 , dan x > 4}
* PERTIDAKAMAAN BENTUK AKAR *
Contoh : √(ax + b) < √(cx + d)
Langkah2 Penyelesaian :
1. ax + b ≥ 0
2. cx + d ≥ 0
3. √(ax + b) < √(cx + d)
Kedua ruas dikuadratkan
4. Hasil dari 1,2,3 diletakkan pada garis bilangan
5. Tentukan HP
1. √(x - 3) < 2
Jawaban :
a. x - 3 ≥ 0 dan b. Tidak ada
x ≥ 3
c. {√(x - 3)}2 < (2)2
x - 3 < 4
x < 7
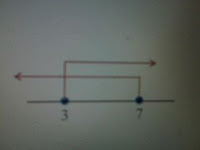
d. pada gambar di samping
e. HP {x│3 < x < 7, x € R}
2. √(x + 2) < √(8 - 2x)
a. x + 2 ≥ 0 dan b. 8 - 2x ≥ 0
x ≥ -2 x ≤ 4
c. {√(x + 2)}2 < {√(8 - 2x)}2
x + 2 < 8 - 2x
3x < 6
x < 2
d. pada gambar di samping
e. HP {x│2 < x ≤ 4}
3. √(x2 + 2x - 3) < x + 2
Jawaban :
(x +3)(x - 1) ≥ 0
x + 3 ≥ 0 atau x - 1 ≥ 0
x ≥ -3 x ≥ 1
b. x + 2 ≥ 0
x ≥ -2
c. {√(x + 2x - 3)}2 < (x + 2)2
x2 + 2x - 3 < x2 + 4x + 4
-2x < 7
x > -7/2
d. Pada gambar disamping
e. HP {x│x ≥ 1, x € R}
* PRTIDAKSAMAAN BENTUK MUTLAK *
│x│ = 1. x, Untuk x > 0 => │5│ = 5
2. -x, Untuk x < 0 => │-5│= -(-5) = 5
3. 0, Untuk x = 0 => │0│ = 0
keteragan : jika │x│≤ a, maka -a ≤ x ≤ a
jika │x│ > a, maka x ≥ a atau x ≤ a
1. │x│< 3
Jawaban :
Cara 1
-3 < x -2 < 3
x - 2 > -3 dan x - 2 < 3
x > -1 x < 5
(x - 2) < 3
x - 4x + 4 < 9
x - 4x - 5 < 0
(x - 5)(x + 1) < 0
x = 5 , x = -1HP {x│-1 < x < 5, x € R}













11 Maret 2014 pukul 09.02
berguna bnget thx yoo :)